復合材料結構件中，不同結構組分可通過共固化或膠接共固化途徑結為一體，以取代緊固件連接方式。此狀態(tài)下，在共固化或膠接共固化界面周邊，形成一個特殊的接頭區(qū)。所謂復合材料整體化結構，即為內(nèi)含此類接頭的復合材料結構型式，圖1給出了典型接頭及其載荷示意。



在整體化結構接頭內(nèi)部，由于載荷傳遞路徑的特殊性，有可能形成不容忽視的層間應力區(qū)（包括層間正應力和層間剪切應力）。該區(qū)層間應力在量值上可能小于結構承受的面內(nèi)應力，但由于復合材料對層間應力的敏感性，破壞則往往由此開始產(chǎn)生（圖2）。層間應力導致的破壞模式是整體化結構接頭的一個重要力學行為特點。有關接頭承載能力的評估需給予特殊關注。

123456
圖2 接頭部位因?qū)娱g應力導致的破壞模式

接頭結構方案的合理與否，取決于對相關結構參數(shù)影響作用的認識程度。這些參數(shù)既涉及接頭的幾何特征（如突緣的長度、填充區(qū)半徑等），同時包括接頭各部位鋪層的構成（如主鋪層的數(shù)量、角度，插層的數(shù)量、角度、插入位置等）。一定載荷條件下，不同的參數(shù)組合方式會導致不同的應力分布狀態(tài)。在設計給定的限制范圍內(nèi)，如何調(diào)配結構參數(shù)的組合以盡可能緩解層間應力水平，是提升接頭承載能力的關鍵所在。

解決問題最直接的方法是設計一系列用以評估結構參數(shù)影響作用的試驗。根據(jù)試驗結果，確定最佳的結構參數(shù)組合方式。但面臨的直接問題是試驗工作量，其時間耗費和經(jīng)濟代價均不容小視。在此情形下，計算機模擬有可能成為解決問題的一條適宜途徑。

接頭力學行為分析模型的相關問題

123,123

由于接頭形狀的復雜性，其力學行為模擬的數(shù)值計算需通過有限元方法實現(xiàn)。因涉及層間應力問題，層合板理論和相應的層合板殼單元不再適用，建模的基礎需回歸到實體單元。
對層合復合材料結構進行三維分析，相對精確的處理方法是將各鋪層假設為均勻的正交各向異性材料，網(wǎng)格的劃分逐層進行。如此建模面臨的一個主要技術問題是接頭總體尺寸與單個鋪層厚度之間的巨大差異。為控制每個單元各向尺寸的比例，不得不構建極為細密的網(wǎng)格，從而給網(wǎng)格劃分計算和有限元求解造成一定麻煩。
針對上述問題，一種簡化處理方法是將多個鋪層合并為一個在剛度上等效的正交各向異性材料鋪層，以此提升對單元尺寸起決定作用的鋪層厚度，從而減少單元的總體數(shù)量。但在采用這種方法時，需對兩方面的問題作細致考慮。
（1）由多個不同取向正交各向異性鋪層組成的疊層塊的剛度行為，實際上無法與單一正交各向異性材料的剛度行為形成完全的等效。因此，即使僅就剛度而言，所謂“等效”也只是一種近似的替代。
（2）即便接受剛度等效引起的偏差，當將模型用于承載能力分析時， 由于無法直接得到各鋪層實際的應力分布，基于單層材料強度參數(shù)的破壞判據(jù)不能直接適用，從而不得不做相應補充工作。比如，結合理論計算和試驗來形成等效材料的三維最大應變判據(jù)。或者，先通過對剛度等效模型的分析結果，確定一系列處于“危險”狀態(tài)的單元。再基于“子模型”概念，對危險單元按其實際的鋪層構成做進一步網(wǎng)格劃分，并以剛度等效計算得到的節(jié)點位移為邊界條件，求解各鋪層的應力應變數(shù)據(jù)。經(jīng)此處理后，可采用真實鋪層的強度參數(shù)和相應破壞判據(jù)來對“危險”單元進行強度裕度評估，以此確定初始損傷單元和相應的載荷水平。

盡管存在上述簡化處理方法，但在計算機硬件和計算時間允許的條件下，仍建議采用逐層網(wǎng)格劃分的方法來進行分析模型構建，以盡可能保證數(shù)學模型與實際結構的近似性。 本文來自123

接頭力學行為分析涉及的另一個重要問題是破壞判據(jù)。實際上，很難建立一套單一的判據(jù)來對任何形式接頭案例的破環(huán)載荷實現(xiàn)精確預測。針對不同的接頭類型和載荷形式，分門別類地形成相應的強度預測準則可能是提升預測準確度的唯一途徑。但當上述條件不完備時，基于Hashin三維失效準則的破壞判據(jù)不失為承載能力預估的有效工具。但在分析結果的預期上，建議對以下因素加以考慮。
（1）當用于結構方案對比，或結構參數(shù)對接頭承載能力影響作用分析時，所得預測結果可較好地反映真實的優(yōu)劣狀況或影響規(guī)律態(tài)勢。當計算機模擬的目標定位于對結構參數(shù)影響作用的評估和對參數(shù)組合的優(yōu)化時，采用按鋪層細分的實體單元與Hashin三維失效準則相結合的方法，可得到有效的模擬或優(yōu)化結果。
（2）就單個案例的計算結果而言，采用按鋪層細分的實體單元與Hashin三維失效準則相結合的方法，所得到的破壞載荷預測值與試驗值之間有可能很好擬合（差異小于10%），也有可能出現(xiàn)較大偏離（差異達到30%以上）。差異的原因一方面源于方法本身。比如，對厚度突變部位（如突緣端部）承載能力的預測值會低于實際情況。當初試破壞由該處應力主導時，接頭的預測破壞載荷會相應偏低。另一方面，接頭特殊的破壞模式和試驗數(shù)量方面的局限，也可能成為導致差異的作用因素。接頭的破壞多始于層間應力導致的脫粘或分層，這種破壞與結構局部的的細觀狀態(tài)（如樹脂含量、孔隙率、殘余應力等）密切相關。相較于纖維破壞導致的結構失效，隨機因素的影響作用顯著突出。即便對于同一批試件，試驗得到的破壞載荷數(shù)據(jù)也往往存在相當大的分散性。因此，合理評估算法對某一類接頭案例評估的準確程度需基于大量試樣的統(tǒng)計結果。單一試樣的試驗值與預測值的對比往往缺乏普遍性的評判意義。 123,123

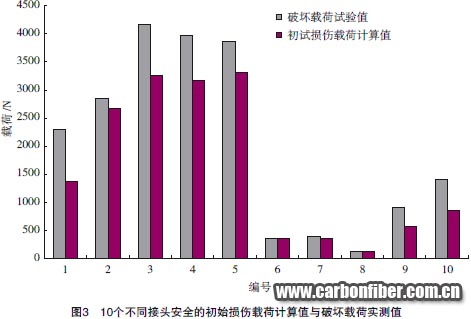
以初始損傷載荷還是破壞載荷來表征接頭的承載能力，也是接頭力學行為模擬涉及的一個具體問題。對破壞載荷的預測不存在特殊的技術困難。實際上，描述復合材料破壞過程的各種算法模型在許多工作中得到應用。但時間耗費是破壞載荷計算的一個主要問題。當分析目標是一個給定的結構案例時，計算時間的影響作用并不凸現(xiàn)。但當分析目標是結構參數(shù)變化的影響作用評估或結構方案的優(yōu)化時，由于涉及大量案例的反復計算，采用破壞載荷作為承載能力表征會使計算時間的耗費變得難以接受。在這種情況下，建議采用初始損傷載荷作為目標函數(shù)。初始損傷載荷和破壞載荷分別處于破壞過程兩端，一般情況下兩者之間會存在差異，差異的幅度也隨結構參數(shù)和載荷條件的不同而變化。但就結構方案的比較而言，初始損傷載荷的計算值可以切實反映承載能力的優(yōu)劣狀況。圖3給出一系列不同形式、不同參數(shù)、不同載荷形式的接頭案例，由試驗測得的破壞載荷與通過計算得到的初始損傷載荷。從圖3可見，在案例承載能力的橫向比較上，初始損傷載荷計算值和破壞載荷實測值反映了基本一致的優(yōu)劣態(tài)勢。



接頭結構參數(shù)影響作用的評估與結構方案的優(yōu)化

接頭結構參數(shù)影響作用的評估與結構方案的優(yōu)化是計算機模擬用于接頭設計可以發(fā)揮的主要作用所在。
接頭結構參數(shù)影響作用評估提供下述模擬結果：對于給定的結構方案，在給定載荷方式下，當結構的某項參數(shù)（如突緣的長度、填充區(qū)半徑、插層的添減、某一插層的端部位置等等）發(fā)生變化時，其承載能力的變化趨勢。

接頭結構參數(shù)優(yōu)化提供下述模擬結果：在給定的設計限制條件下（通常為各項參數(shù)的變化范圍及載荷形式），以承載能力為目標，給出較優(yōu)的參數(shù)組合。
進行接頭結構參數(shù)影響作用評估時，算法的總體框架比較簡單。僅需對所分析參數(shù)設置合理的變化區(qū)間，并在該區(qū)間內(nèi)對參數(shù)進行離散處理，形成對應的接頭結構案例。對案例逐一計算承載能力， 可得到描述結構參數(shù)影響作用的函數(shù)曲線。根據(jù)曲線各部位斜率，可給出影響作用的評估結論。 內(nèi)容來自123456
當工作目標為接頭結構參數(shù)的優(yōu)化時，算法所涉及的問題相對復雜。在設計給定的參數(shù)限制范圍內(nèi)，如對各項參數(shù)作離散化處理，計算對象即成為離散事件的組合最優(yōu)化問題。將基于啟發(fā)式方法的現(xiàn)代優(yōu)化算法納入計算過程，理論上不存在絕對無法解決的困難。但由于接頭結構參數(shù)的多變量特點，以及目標函數(shù)計算過程的復雜性（對可行解的目標函數(shù)計算實際上等同于對一個結構案例的有限元分析計算），即便采用初始損傷載荷作為承載能力表征，時間代價仍可能成為一個不容忽視的負面因素。要對這方面進行改善，算法設計需要尋求其他途徑。一個建議方向是將試驗設計方法引入模擬過程。其基本思路是參照試驗設計理論（如Taguchi方法等），規(guī)劃一系列反映不同參數(shù)組合的試驗案例，把對每個案例的有限元計算結果視為一次模擬試驗結果，根據(jù)各項參數(shù)的因子反應分析，來得到一個較優(yōu)的參數(shù)組合結果。由于減免了優(yōu)化解搜尋涉及的計算工作量，計算時間可得到顯著縮短。 123,123
無論是結構參數(shù)影響作用評估，還是結構參數(shù)的組合優(yōu)化，其實現(xiàn)過程共同面臨的一個技術問題是有限元模型的自動構建。計算過程會生成大量反映不同參數(shù)組合的計算案例，每個案例均需根據(jù)特定的結構參數(shù)組合方式構建相應的有限元模型。顯然，即便在各種建模工具的充分支持下，通過人工來完成每個模型的構建，實際上也是難以實現(xiàn)的。因此，根據(jù)特定的結構參數(shù)組合方式，來完全自動地實現(xiàn)接頭有限元模型構建的計算程序模塊，是實現(xiàn)模擬工作目標不可或缺的基本技術支撐。
自動建模算法須能根據(jù)一系列給定的幾何參數(shù)和鋪層參數(shù)，為接頭內(nèi)每一鋪層（包括插層）和每一填充區(qū)構建合理的分析網(wǎng)格，同時滿足各鋪層網(wǎng)格相互結合部的節(jié)點共有要求。此外，需能準確構建每個單元的材料坐標系。圖4給出通過專門設計的算法，在模擬接頭突緣和突緣區(qū)底板內(nèi)部增減插層對承載能力影響作用的計算過程中，自動生成了部分模型示意圖。 copyright 123456


圖4 反應不同參數(shù)組合的一系列分析模式

應該指出的是，真實的結構應用場合中，在與圖1平面垂直的方向上（以下簡稱為長度向），接頭的長度一般會遠大于如圖4模型所示尺寸。圖4所給模型實際上代表的是一個從完整結構中截出的接頭部分。通常，要對一個完整的接頭結構（比如一個在長度向延伸2m的接頭）進行模擬計算，從實用性角度看，相應的時間耗費很難被接受。因此，與結構元件試驗相似，模擬計算希望借助一個與完整結構分離的元件模型來評估元件所反映的設計概念被用于完整結構的利弊得失。而在此狀況下，如何根據(jù)完整結構的載荷狀況來合理設置模型各相關截面上的載荷或邊界條件，是一個需要仔細斟酌的問題（比如，圖4模型中與長度向垂直的前、后表面應施以何種邊界條件？）。必要時，可通過對完整結構的粗略分析（如層合殼單元分析或尺寸相對較大的等效剛度實體單元分析）來得到每個相關截面上的節(jié)點位移狀態(tài)，并將此作為元件模型的邊界條件，以得到與實際應用環(huán)境更為相符的模擬和評估結果。
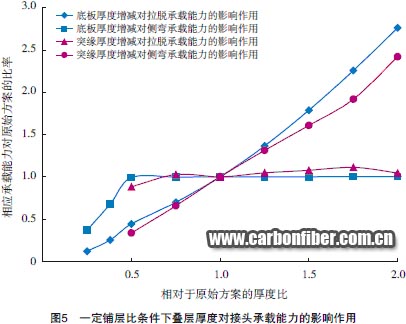
圖5為一原始接頭方案，在給定鋪層比條件下增減其填充區(qū)周邊突緣疊層厚度或底板疊層厚度，承載能力所受影響作用的模擬結果。可以看到，接頭結構參數(shù)在一定范圍內(nèi)變化可對承載能力形成顯著影響，并且影響作用會隨載荷形式的不同而發(fā)生明顯差異。由于本文的綜述性質(zhì)，此處不對影響作用的具體細節(jié)進行討論，僅通過圖例表明其復雜性。同時表明，對于接頭的合理設計，模擬結果可提供方向性的參數(shù)修正依據(jù)。



結束語

將計算機模擬技術用于復合材料整體化結構的接頭設計，如將預期功效定位于結構參數(shù)變化對結構行為的影響作用，可以起到很好的實際輔助作用。需要特別強調(diào)的是，具體的應用背景會對結構參數(shù)的形式和變化范圍提出具體的要求或限制范圍。因此，相關的模型和算法只有在與結構設計人員的反復互動過程中才能得到反復的完善，從而獲得真正符合設計人員需求的使用效益。另一方面，如文中多次提及，計算時間的長短會非常顯著地影響模擬方法的實用程度。對工程技術而言，“簡捷”的重要性在許多場合并不亞于“精確”。兩者雖往往不可兼得，但需時時兼顧。而對兩者權衡的深思熟慮程度，有可能左右模擬方法或模擬工具在實際工程應用中的成敗。（責編　良辰）